Tutorial 1: Neural Rate Models#
Week 2, Day 4: Dynamic Networks
By Neuromatch Academy
Content creators: Qinglong Gu, Songtin Li, Arvind Kumar, John Murray, Julijana Gjorgjieva
Content reviewers: Maryam Vaziri-Pashkam, Ella Batty, Lorenzo Fontolan, Richard Gao, Spiros Chavlis, Michael Waskom, Siddharth Suresh
Production editors: Gagana B, Spiros Chavlis
Tutorial Objectives#
Estimated timing of tutorial: 1 hour, 25 minutes
The brain is a complex system, not because it is composed of a large number of diverse types of neurons, but mainly because of how neurons are connected to each other. The brain is indeed a network of highly specialized neuronal networks.
The activity of a neural network constantly evolves in time. For this reason, neurons can be modeled as dynamical systems. The dynamical system approach is only one of the many modeling approaches that computational neuroscientists have developed (other points of view include information processing, statistical models, etc.).
How the dynamics of neuronal networks affect the representation and processing of information in the brain is an open question. However, signatures of altered brain dynamics present in many brain diseases (e.g., in epilepsy or Parkinson’s disease) tell us that it is crucial to study network activity dynamics if we want to understand the brain.
In this tutorial, we will simulate and study one of the simplest models of biological neuronal networks. Instead of modeling and simulating individual excitatory neurons (e.g., LIF models that you implemented yesterday), we will treat them as a single homogeneous population and approximate their dynamics using a single one-dimensional equation describing the evolution of their average spiking rate in time.
In this tutorial, we will learn how to build a firing rate model of a single population of excitatory neurons.
Steps:
Write the equation for the firing rate dynamics of a 1D excitatory population.
Visualize the response of the population as a function of parameters such as threshold level and gain, using the frequency-current (F-I) curve.
Numerically simulate the dynamics of the excitatory population and find the fixed points of the system.
Setup#
Install and import feedback gadget#
Show code cell source
# @title Install and import feedback gadget
!pip3 install vibecheck datatops --quiet
from vibecheck import DatatopsContentReviewContainer
def content_review(notebook_section: str):
return DatatopsContentReviewContainer(
"", # No text prompt
notebook_section,
{
"url": "https://pmyvdlilci.execute-api.us-east-1.amazonaws.com/klab",
"name": "neuromatch_cn",
"user_key": "y1x3mpx5",
},
).render()
feedback_prefix = "W2D4_T1"
# Imports
import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize as opt # root-finding algorithm
Figure Settings#
Show code cell source
# @title Figure Settings
import logging
logging.getLogger('matplotlib.font_manager').disabled = True
import ipywidgets as widgets # interactive display
%config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/main/nma.mplstyle")
Plotting Functions#
Show code cell source
# @title Plotting Functions
def plot_fI(x, f):
plt.figure(figsize=(6, 4)) # plot the figure
plt.plot(x, f, 'k')
plt.xlabel('x (a.u.)', fontsize=14)
plt.ylabel('F(x)', fontsize=14)
plt.show()
def plot_dr_r(r, drdt, x_fps=None):
plt.figure()
plt.plot(r, drdt, 'k')
plt.plot(r, 0. * r, 'k--')
if x_fps is not None:
plt.plot(x_fps, np.zeros_like(x_fps), "ko", ms=12)
plt.xlabel(r'$r$')
plt.ylabel(r'$\frac{dr}{dt}$', fontsize=20)
plt.ylim(-0.1, 0.1)
plt.show()
def plot_dFdt(x, dFdt):
plt.figure()
plt.plot(x, dFdt, 'r')
plt.xlabel('x (a.u.)', fontsize=14)
plt.ylabel('dF(x)', fontsize=14)
plt.show()
Section 1: Neuronal network dynamics#
Video 1: Dynamic networks#
This video covers how to model a network with a single population of neurons and introduces neural rate-based models. It overviews feedforward networks and defines the F-I (firing rate vs. input) curve.
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Dynamic_networks_Video")
Section 1.1: Dynamics of a single excitatory population#
Click here for text recap of relevant part of video
Individual neurons respond by spiking. When we average the spikes of neurons in a population, we can define the average firing activity of the population. In this model, we are interested in how the population-averaged firing varies as a function of time and network parameters. Mathematically, we can describe the firing rate dynamic of a feed-forward network as:
\(r(t)\) represents the average firing rate of the excitatory population at time \(t\), \(\tau\) controls the timescale of the evolution of the average firing rate, \(I_{\text{ext}}\) represents the external input, and the transfer function \(F(\cdot)\) (which can be related to f-I curve of individual neurons described in the next sections) represents the population activation function in response to all received inputs.
To start building the model, please execute the cell below to initialize the simulation parameters.
Execute this cell to set default parameters for a single excitatory population model
Show code cell source
# @markdown *Execute this cell to set default parameters for a single excitatory population model*
def default_pars_single(**kwargs):
pars = {}
# Excitatory parameters
pars['tau'] = 1. # Timescale of the E population [ms]
pars['a'] = 1.2 # Gain of the E population
pars['theta'] = 2.8 # Threshold of the E population
# Connection strength
pars['w'] = 0. # E to E, we first set it to 0
# External input
pars['I_ext'] = 0.
# simulation parameters
pars['T'] = 20. # Total duration of simulation [ms]
pars['dt'] = .1 # Simulation time step [ms]
pars['r_init'] = 0.2 # Initial value of E
# External parameters if any
pars.update(kwargs)
# Vector of discretized time points [ms]
pars['range_t'] = np.arange(0, pars['T'], pars['dt'])
return pars
pars = default_pars_single()
print(pars)
{'tau': 1.0, 'a': 1.2, 'theta': 2.8, 'w': 0.0, 'I_ext': 0.0, 'T': 20.0, 'dt': 0.1, 'r_init': 0.2, 'range_t': array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ,
1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. , 2.1,
2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2,
3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. , 4.1, 4.2, 4.3,
4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5. , 5.1, 5.2, 5.3, 5.4,
5.5, 5.6, 5.7, 5.8, 5.9, 6. , 6.1, 6.2, 6.3, 6.4, 6.5,
6.6, 6.7, 6.8, 6.9, 7. , 7.1, 7.2, 7.3, 7.4, 7.5, 7.6,
7.7, 7.8, 7.9, 8. , 8.1, 8.2, 8.3, 8.4, 8.5, 8.6, 8.7,
8.8, 8.9, 9. , 9.1, 9.2, 9.3, 9.4, 9.5, 9.6, 9.7, 9.8,
9.9, 10. , 10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9,
11. , 11.1, 11.2, 11.3, 11.4, 11.5, 11.6, 11.7, 11.8, 11.9, 12. ,
12.1, 12.2, 12.3, 12.4, 12.5, 12.6, 12.7, 12.8, 12.9, 13. , 13.1,
13.2, 13.3, 13.4, 13.5, 13.6, 13.7, 13.8, 13.9, 14. , 14.1, 14.2,
14.3, 14.4, 14.5, 14.6, 14.7, 14.8, 14.9, 15. , 15.1, 15.2, 15.3,
15.4, 15.5, 15.6, 15.7, 15.8, 15.9, 16. , 16.1, 16.2, 16.3, 16.4,
16.5, 16.6, 16.7, 16.8, 16.9, 17. , 17.1, 17.2, 17.3, 17.4, 17.5,
17.6, 17.7, 17.8, 17.9, 18. , 18.1, 18.2, 18.3, 18.4, 18.5, 18.6,
18.7, 18.8, 18.9, 19. , 19.1, 19.2, 19.3, 19.4, 19.5, 19.6, 19.7,
19.8, 19.9])}
You can now use:
pars = default_pars_single()to get all the parameters.pars = default_pars_single(T=T_sim, dt=time_step)to set new simulation time and time stepTo update an existing parameter dictionary, use
pars['New_para'] = value
Because pars is a dictionary, it can be passed to a function that requires individual parameters as arguments using my_func(**pars) syntax.
Section 1.2: F-I curves#
Estimated timing to here from start of tutorial: 17 min
Click here for text recap of relevant part of video
In electrophysiology, a neuron is often characterized by its spike rate output in response to input currents. This is often called the F-I curve, denoting the output spike frequency (F) in response to different injected currents (I). We estimated this for an LIF neuron in yesterday’s tutorial.
The transfer function \(F(\cdot)\) in Equation \(1\) represents the gain of the population as a function of the total input. The gain is often modeled as a sigmoidal function, i.e., more input drive leads to a nonlinear increase in the population firing rate. The output firing rate will eventually saturate for high input values.
A sigmoidal \(F(\cdot)\) is parameterized by its gain \(a\) and threshold \(\theta\).
The argument \(x\) represents the input to the population. Note that the second term is chosen so that \(F(0;a,\theta)=0\).
Many other transfer functions (generally monotonic) can be also used. Examples are the rectified linear function \(ReLU(x)\) or the hyperbolic tangent \(tanh(x)\).
Coding Exercise 1.2: Implement F-I curve#
Let’s first investigate the activation functions before simulating the dynamics of the entire population.
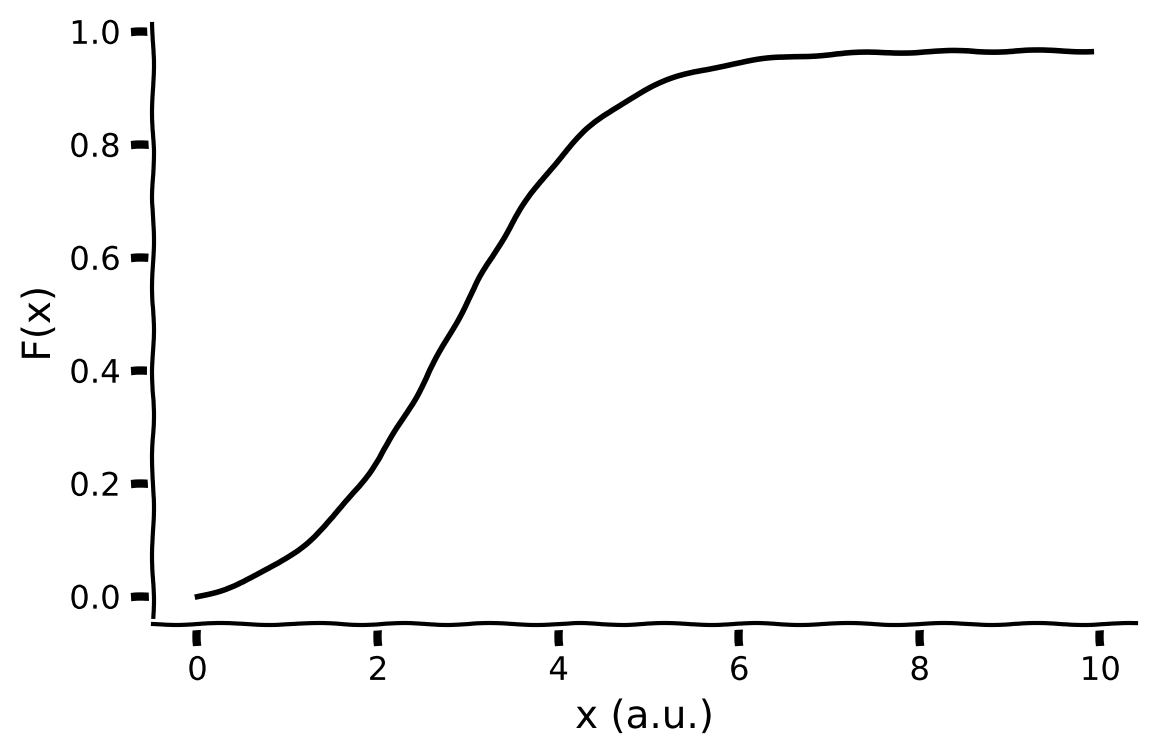
In this exercise, you will implement a sigmoidal F-I curve or transfer function \(F(x)\), with gain \(a\) and threshold level \(\theta\) as parameters:
def F(x, a, theta):
"""
Population activation function.
Args:
x (float): the population input
a (float): the gain of the function
theta (float): the threshold of the function
Returns:
float: the population activation response F(x) for input x
"""
#################################################
## TODO for students: compute f = F(x) ##
# Fill out function and remove
raise NotImplementedError("Student exercise: implement the f-I function")
#################################################
# Define the sigmoidal transfer function f = F(x)
f = ...
return f
# Set parameters
pars = default_pars_single() # get default parameters
x = np.arange(0, 10, .1) # set the range of input
# Compute transfer function
f = F(x, pars['a'], pars['theta'])
# Visualize
plot_fI(x, f)
Example output:
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Implement_FI_curve_Exercise")
Interactive Demo 1.2 : Parameter exploration of F-I curve#
Here’s an interactive demo that shows how the F-I curve changes for different values of the gain and threshold parameters.
How does the gain parameter (\(a\)) affect the F-I curve?
How does the threshold parameter (\(\theta\)) affect the F-I curve?
Make sure you execute this cell to enable the widget!
Show code cell source
# @markdown Make sure you execute this cell to enable the widget!
@widgets.interact(
a=widgets.FloatSlider(1.5, min=0.3, max=3., step=0.3),
theta=widgets.FloatSlider(3., min=2., max=4., step=0.2)
)
def interactive_plot_FI(a, theta):
"""
Population activation function.
Expecxts:
a : the gain of the function
theta : the threshold of the function
Returns:
plot the F-I curve with give parameters
"""
# set the range of input
x = np.arange(0, 10, .1)
plt.figure()
plt.plot(x, F(x, a, theta), 'k')
plt.xlabel('x (a.u.)', fontsize=14)
plt.ylabel('F(x)', fontsize=14)
plt.show()
<Figure size 800x600 with 0 Axes>
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Parameter_exploration_of_FI_curve_Interactive_Demo_and_Discussion")
Section 1.3: Simulation scheme of E dynamics#
Estimated timing to here from start of tutorial: 27 min
Because \(F(\cdot)\) is a nonlinear function, the exact solution of our differential equation of population activity can not be determined via analytical methods. As we have seen before, we can use numerical methods, specifically the Euler method, to find the solution (that is, simulate the population activity).
Execute this cell to enable the single population rate model simulator: simulate_single
Show code cell source
# @markdown Execute this cell to enable the single population rate model simulator: `simulate_single`
def simulate_single(pars):
"""
Simulate an excitatory population of neurons
Args:
pars : Parameter dictionary
Returns:
rE : Activity of excitatory population (array)
Example:
pars = default_pars_single()
r = simulate_single(pars)
"""
# Set parameters
tau, a, theta = pars['tau'], pars['a'], pars['theta']
w = pars['w']
I_ext = pars['I_ext']
r_init = pars['r_init']
dt, range_t = pars['dt'], pars['range_t']
Lt = range_t.size
# Initialize activity
r = np.zeros(Lt)
r[0] = r_init
I_ext = I_ext * np.ones(Lt)
# Update the E activity
for k in range(Lt - 1):
dr = dt / tau * (-r[k] + F(w * r[k] + I_ext[k], a, theta))
r[k+1] = r[k] + dr
return r
help(simulate_single)
Help on function simulate_single in module __main__:
simulate_single(pars)
Simulate an excitatory population of neurons
Args:
pars : Parameter dictionary
Returns:
rE : Activity of excitatory population (array)
Example:
pars = default_pars_single()
r = simulate_single(pars)
Interactive Demo 1.3: Parameter Exploration of single population dynamics#
Explore these dynamics of the population activity in this interactive demo.
How does \(r_{\text{sim}}(t)\) change with different \(I_{\text{ext}}\) values?
How does it change with different \(\tau\) values?
Note that, \(r_{\rm ana}(t)\) denotes the analytical solution - you will learn how this is computed in the next section.
#
Make sure you execute this cell to enable the widget!
Show code cell source
# @title
# @markdown Make sure you execute this cell to enable the widget!
# get default parameters
pars = default_pars_single(T=20.)
@widgets.interact(
I_ext=widgets.FloatSlider(5.0, min=0.0, max=10., step=1.),
tau=widgets.FloatSlider(3., min=1., max=5., step=0.2)
)
def Myplot_E_diffI_difftau(I_ext, tau):
# set external input and time constant
pars['I_ext'] = I_ext
pars['tau'] = tau
# simulation
r = simulate_single(pars)
# Analytical Solution
r_ana = (pars['r_init']
+ (F(I_ext, pars['a'], pars['theta'])
- pars['r_init']) * (1. - np.exp(-pars['range_t'] / pars['tau'])))
# plot
plt.figure()
plt.plot(pars['range_t'], r, 'b', label=r'$r_{\mathrm{sim}}$(t)', alpha=0.5,
zorder=1)
plt.plot(pars['range_t'], r_ana, 'b--', lw=5, dashes=(2, 2),
label=r'$r_{\mathrm{ana}}$(t)', zorder=2)
plt.plot(pars['range_t'],
F(I_ext, pars['a'], pars['theta']) * np.ones(pars['range_t'].size),
'k--', label=r'$F(I_{\mathrm{ext}})$')
plt.xlabel('t (ms)', fontsize=16.)
plt.ylabel('Activity r(t)', fontsize=16.)
plt.legend(loc='best', fontsize=14.)
plt.show()
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Parameter_exploration_of_single_population_dynamics_Interactive_Demo_and_Discussion")
Think! 1.3: Finite activities#
Above, we have numerically solved a system driven by a positive input. Yet, \(r_E(t)\) either decays to zero or reaches a fixed non-zero value.
Why doesn’t the solution of the system “explode” in a finite time? In other words, what guarantees that \(r_E\)(t) stays finite?
Which parameter would you change in order to increase the maximum value of the response?
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Finite_activities_Discussion")
Section 2: Fixed points of the single population system#
Estimated timing to here from start of tutorial: 45 min
Section 2.1: Finding fixed points#
Video 2: Fixed point#
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Finding_fixed_points_Video")
This video introduces recurrent networks and how to derive their fixed points. It also introduces vector fields and phase planes in one dimension.
Click here for text recap of video
We can now extend our feed-forward network to a recurrent network, governed by the equation:
where as before, \(r(t)\) represents the average firing rate of the excitatory population at time \(t\), \(\tau\) controls the timescale of the evolution of the average firing rate, \(I_{\text{ext}}\) represents the external input, and the transfer function \(F(\cdot)\) (which can be related to f-I curve of individual neurons described in the next sections) represents the population activation function in response to all received inputs. Now we also have \(w\) which denotes the strength (synaptic weight) of the recurrent input to the population.
As you varied the two parameters in the last Interactive Demo, you noticed that, while at first the system output quickly changes, with time, it reaches its maximum/minimum value and does not change anymore. The value eventually reached by the system is called the steady state of the system, or the fixed point. Essentially, in the steady states the derivative with respect to time of the activity (\(r\)) is zero, i.e. \(\displaystyle \frac{dr}{dt}=0\).
We can find that the steady state of the Equation. (1) by setting \(\displaystyle{\frac{dr}{dt}=0}\) and solve for \(r\):
When it exists, the solution of Equation. (4) defines a fixed point of the dynamical system in Equation (3). Note that if \(F(x)\) is nonlinear, it is not always possible to find an analytical solution, but the solution can be found via numerical simulations, as we will do later.
From the Interactive Demo, one could also notice that the value of \(\tau\) influences how quickly the activity will converge to the steady state from its initial value.
In the specific case of \(w=0\), we can also analytically compute the solution of Equation (1) (i.e., the thick blue dashed line) and deduce the role of \(\tau\) in determining the convergence to the fixed point:
We can now numerically calculate the fixed point with a root finding algorithm.
Coding Exercise 2.1.1: Visualization of the fixed points#
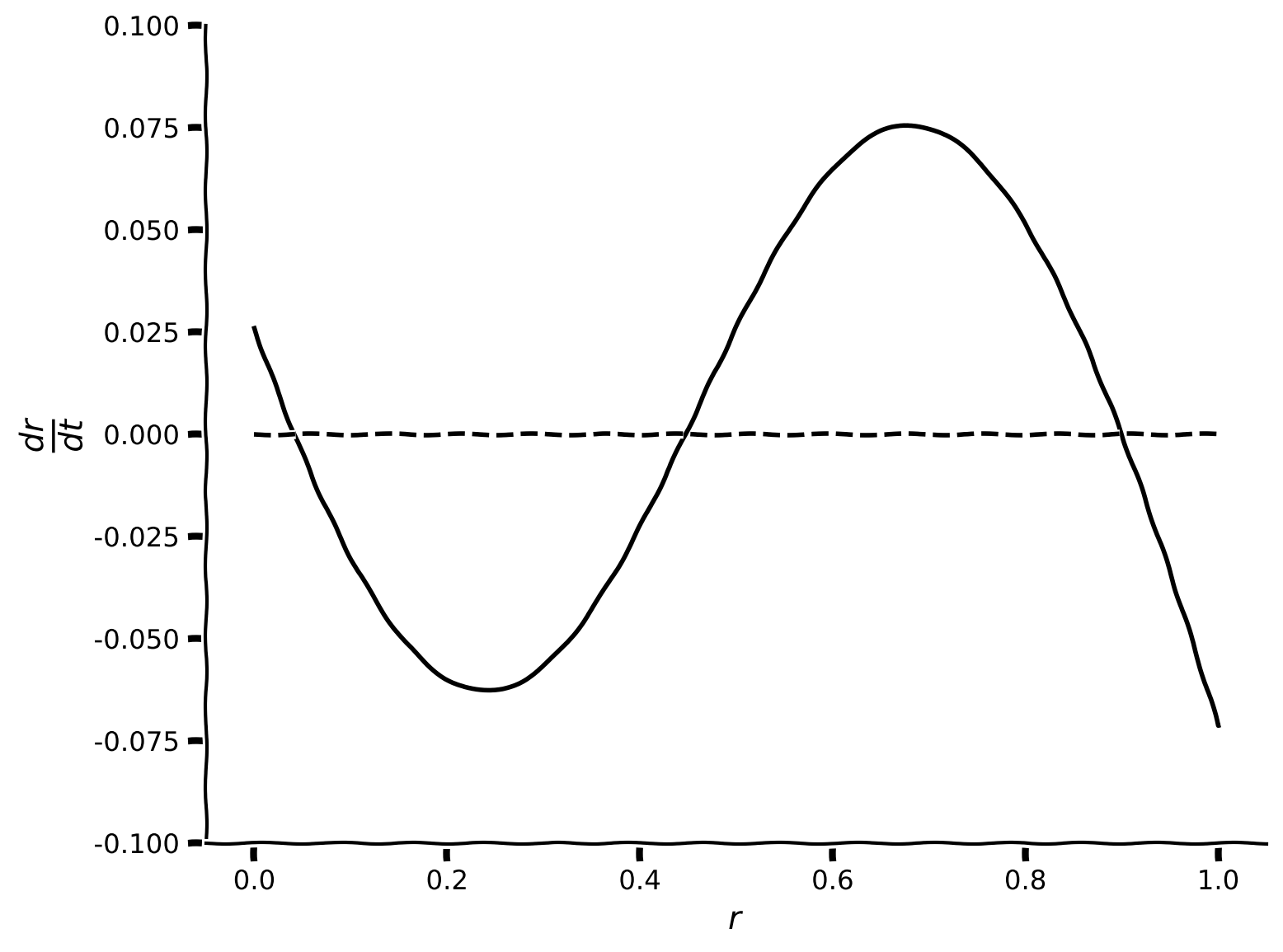
When it is not possible to find the solution for Equation (3) analytically, a graphical approach can be taken. To that end, it is useful to plot \(\displaystyle{\frac{dr}{dt}}\) as a function of \(r\). The values of \(r\) for which the plotted function crosses zero on the y axis correspond to fixed points.
Here, let us, for example, set \(w=5.0\) and \(I^{\text{ext}}=0.5\). From Equation (3), you can obtain
Then, plot the \(dr/dt\) as a function of \(r\), and check for the presence of fixed points.
def compute_drdt(r, I_ext, w, a, theta, tau, **other_pars):
"""Given parameters, compute dr/dt as a function of r.
Args:
r (1D array) : Average firing rate of the excitatory population
I_ext, w, a, theta, tau (numbers): Simulation parameters to use
other_pars : Other simulation parameters are unused by this function
Returns
drdt function for each value of r
"""
#########################################################################
# TODO compute drdt and disable the error
raise NotImplementedError("Finish the compute_drdt function")
#########################################################################
# Calculate drdt
drdt = ...
return drdt
# Define a vector of r values and the simulation parameters
r = np.linspace(0, 1, 1000)
pars = default_pars_single(I_ext=0.5, w=5)
# Compute dr/dt
drdt = compute_drdt(r, **pars)
# Visualize
plot_dr_r(r, drdt)
Example output:
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Visualization_of_the_fixed_points_Exercise")
Coding Exercise 2.1.2: Numerical calculation of fixed points#
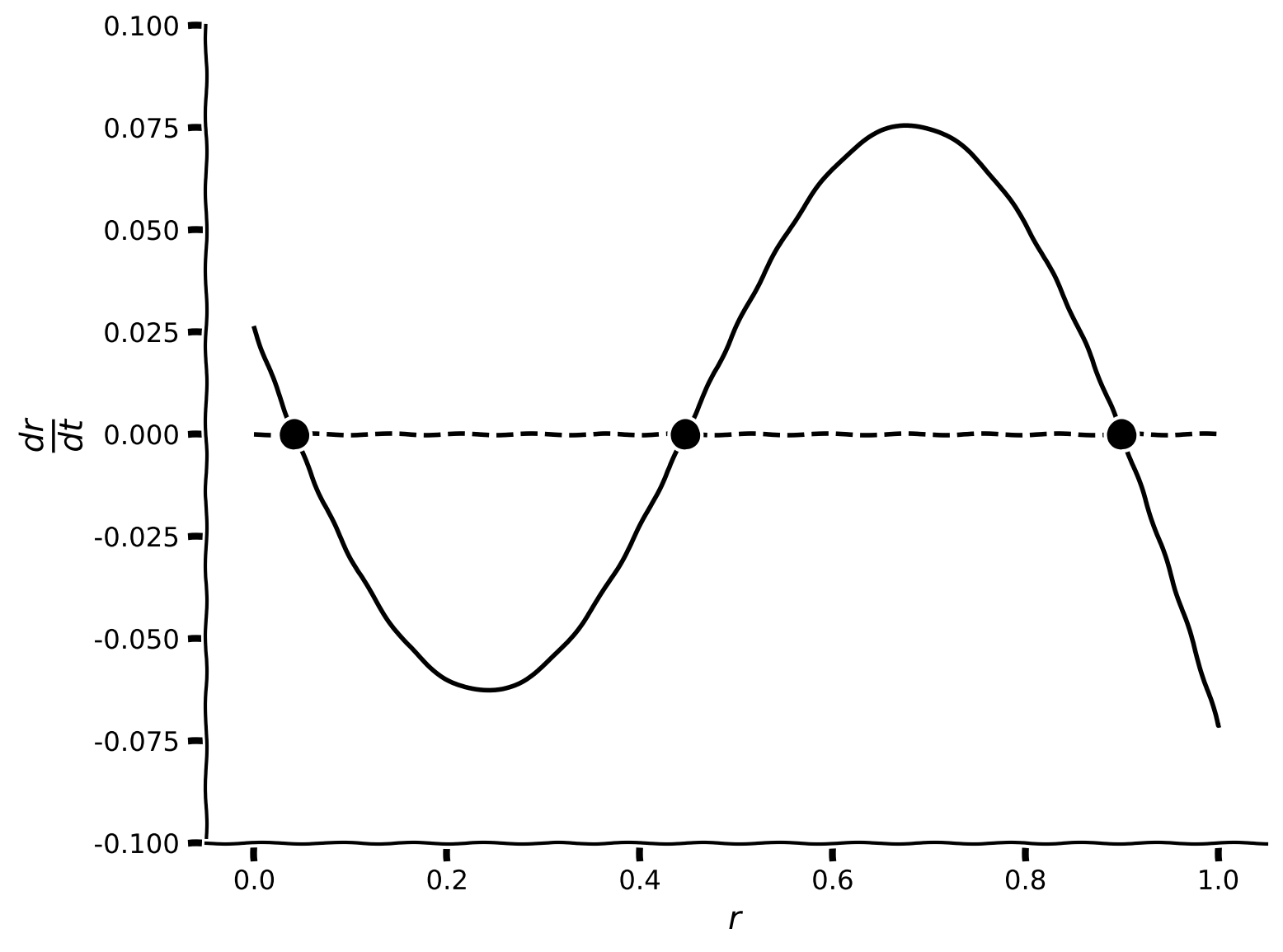
We will now find the fixed points numerically. To do so, we need to specify initial values (\(r_{\text{guess}}\)) for the root-finding algorithm to start from. From the line \(\displaystyle{\frac{dr}{dt}}\) plotted above in the last exercise, initial values can be chosen as a set of values close to where the line crosses zero on the y axis (real fixed point).
The next cell defines three helper functions that we will use:
my_fp_single(r_guess, **pars)uses a root-finding algorithm to locate a fixed point near a given initial valuecheck_fp_single(x_fp, **pars)verifies that the values of \(r_{\rm fp}\) for which \(\displaystyle{\frac{dr}{dt}} = 0\) are the true fixed pointsmy_fp_finder(r_guess_vector, **pars)accepts an array of initial values and finds the same number of fixed points, using the above two functions
Execute this cell to enable the fixed point functions
Show code cell source
# @markdown Execute this cell to enable the fixed point functions
def my_fp_single(r_guess, a, theta, w, I_ext, **other_pars):
"""
Calculate the fixed point through drE/dt=0
Args:
r_guess : Initial value used for scipy.optimize function
a, theta, w, I_ext : simulation parameters
Returns:
x_fp : value of fixed point
"""
# define the right hand of E dynamics
def my_WCr(x):
r = x
drdt = (-r + F(w * r + I_ext, a, theta))
y = np.array(drdt)
return y
x0 = np.array(r_guess)
x_fp = opt.root(my_WCr, x0).x.item()
return x_fp
def check_fp_single(x_fp, a, theta, w, I_ext, mytol=1e-4, **other_pars):
"""
Verify |dr/dt| < mytol
Args:
fp : value of fixed point
a, theta, w, I_ext: simulation parameters
mytol : tolerance, default as 10^{-4}
Returns :
Whether it is a correct fixed point: True/False
"""
# calculate Equation(3)
y = x_fp - F(w * x_fp + I_ext, a, theta)
# Here we set tolerance as 10^{-4}
return np.abs(y) < mytol
def my_fp_finder(pars, r_guess_vector, mytol=1e-4):
"""
Calculate the fixed point(s) through drE/dt=0
Args:
pars : Parameter dictionary
r_guess_vector : Initial values used for scipy.optimize function
mytol : tolerance for checking fixed point, default as 10^{-4}
Returns:
x_fps : values of fixed points
"""
x_fps = []
correct_fps = []
for r_guess in r_guess_vector:
x_fp = my_fp_single(r_guess, **pars)
if check_fp_single(x_fp, **pars, mytol=mytol):
x_fps.append(x_fp)
return x_fps
help(my_fp_finder)
Help on function my_fp_finder in module __main__:
my_fp_finder(pars, r_guess_vector, mytol=0.0001)
Calculate the fixed point(s) through drE/dt=0
Args:
pars : Parameter dictionary
r_guess_vector : Initial values used for scipy.optimize function
mytol : tolerance for checking fixed point, default as 10^{-4}
Returns:
x_fps : values of fixed points
# Set parameters
r = np.linspace(0, 1, 1000)
pars = default_pars_single(I_ext=0.5, w=5)
# Compute dr/dt
drdt = compute_drdt(r, **pars)
#############################################################################
# TODO for students:
# Define initial values close to the intersections of drdt and y=0
# (How many initial values? Hint: How many times do the two lines intersect?)
# Calculate the fixed point with these initial values and plot them
raise NotImplementedError('student_exercise: find fixed points numerically')
#############################################################################
# Initial guesses for fixed points
r_guess_vector = [...]
# Find fixed point numerically
x_fps = my_fp_finder(pars, r_guess_vector)
# Visualize
plot_dr_r(r, drdt, x_fps)
Example output:
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Numerical_calculation_of_fixed_points_Exercise")
Interactive Demo 2.1: fixed points as a function of recurrent and external inputs.#
You can now explore how the previous plot changes when the recurrent coupling \(w\) and the external input \(I_{\text{ext}}\) take different values. How does the number of fixed points change?
Make sure you execute this cell to enable the widget!
Show code cell source
# @markdown Make sure you execute this cell to enable the widget!
@widgets.interact(
w=widgets.FloatSlider(4., min=1., max=7., step=0.2),
I_ext=widgets.FloatSlider(1.5, min=0., max=3., step=0.1)
)
def plot_intersection_single(w, I_ext):
# set your parameters
pars = default_pars_single(w=w, I_ext=I_ext)
# find fixed points
r_init_vector = [0, .4, .9]
x_fps = my_fp_finder(pars, r_init_vector)
# plot
r = np.linspace(0, 1., 1000)
drdt = (-r + F(w * r + I_ext, pars['a'], pars['theta'])) / pars['tau']
plot_dr_r(r, drdt, x_fps)
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Fixed_points_inputs_Interactive_Demo_and_Discussion")
Section 2.2: Relationship between trajectories & fixed points#
Let’s examine the relationship between the population activity over time and the fixed points.
Here, let us first set \(w=5.0\) and \(I_{\text{ext}}=0.5\), and investigate the dynamics of \(r(t)\) starting with different initial values \(r(0) \equiv r_{\text{init}}\).
Execute to visualize dr/dt
Show code cell source
# @markdown Execute to visualize dr/dt
def plot_intersection_single(w, I_ext):
# set your parameters
pars = default_pars_single(w=w, I_ext=I_ext)
# find fixed points
r_init_vector = [0, .4, .9]
x_fps = my_fp_finder(pars, r_init_vector)
# plot
r = np.linspace(0, 1., 1000)
drdt = (-r + F(w * r + I_ext, pars['a'], pars['theta'])) / pars['tau']
plot_dr_r(r, drdt, x_fps)
plot_intersection_single(w = 5.0, I_ext = 0.5)
Interactive Demo 2.2: dynamics as a function of the initial value#
Let’s now set \(r_{\rm init}\) to a value of your choice in this demo. How does the solution change? What do you observe? How does that relate to the previous plot of \(\frac{dr}{dt}\)?
Make sure you execute this cell to enable the widget!
Show code cell source
# @markdown Make sure you execute this cell to enable the widget!
pars = default_pars_single(w=5.0, I_ext=0.5)
@widgets.interact(
r_init=widgets.FloatSlider(0.5, min=0., max=1., step=.02)
)
def plot_single_diffEinit(r_init):
pars['r_init'] = r_init
r = simulate_single(pars)
plt.figure()
plt.plot(pars['range_t'], r, 'b', zorder=1)
plt.plot(0, r[0], 'bo', alpha=0.7, zorder=2)
plt.xlabel('t (ms)', fontsize=16)
plt.ylabel(r'$r(t)$', fontsize=16)
plt.ylim(0, 1.0)
plt.show()
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Dynamics_initial_value_Interactive_Demo_and_Discussion")
We will plot the trajectories of \(r(t)\) with \(r_{\text{init}} = 0.0, 0.1, 0.2,..., 0.9\).
Execute this cell to see the trajectories!
Show code cell source
# @markdown Execute this cell to see the trajectories!
pars = default_pars_single()
pars['w'] = 5.0
pars['I_ext'] = 0.5
plt.figure(figsize=(8, 5))
for ie in range(10):
pars['r_init'] = 0.1 * ie # set the initial value
r = simulate_single(pars) # run the simulation
# plot the activity with given initial
plt.plot(pars['range_t'], r, 'b', alpha=0.1 + 0.1 * ie,
label=r'r$_{\mathrm{init}}$=%.1f' % (0.1 * ie))
plt.xlabel('t (ms)')
plt.title('Two steady states?')
plt.ylabel(r'$r$(t)')
plt.legend(loc=[1.01, -0.06], fontsize=14)
plt.show()
We have three fixed points but only two steady states showing up - what’s happening?
It turns out that the stability of the fixed points matters. If a fixed point is stable, a trajectory starting near that fixed point will stay close to that fixed point and converge to it (the steady state will equal the fixed point). If a fixed point is unstable, any trajectories starting close to it will diverge and go towards stable fixed points. In fact, the only way for a trajectory to reach a stable state at an unstable fixed point is if the initial value exactly equals the value of the fixed point.
Think! 2.2: Stable vs unstable fixed points#
Which of the fixed points for the model we’ve been examining in this section are stable vs unstable?
Execute to print fixed point values
Show code cell source
# @markdown Execute to print fixed point values
# Initial guesses for fixed points
r_guess_vector = [0, .4, .9]
# Find fixed point numerically
x_fps = my_fp_finder(pars, r_guess_vector)
print(f'Our fixed points are {x_fps}')
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Stable_vs_unstable_fixed_points_Discussion")
We can simulate the trajectory if we start at the unstable fixed point: you can see that it remains at that fixed point (the red line below).
Execute to visualize trajectory starting at unstable fixed point
Show code cell source
# @markdown Execute to visualize trajectory starting at unstable fixed point
pars = default_pars_single()
pars['w'] = 5.0
pars['I_ext'] = 0.5
plt.figure(figsize=(8, 5))
for ie in range(10):
pars['r_init'] = 0.1 * ie # set the initial value
r = simulate_single(pars) # run the simulation
# plot the activity with given initial
plt.plot(pars['range_t'], r, 'b', alpha=0.1 + 0.1 * ie,
label=r'r$_{\mathrm{init}}$=%.1f' % (0.1 * ie))
pars['r_init'] = x_fps[1] # set the initial value
r = simulate_single(pars) # run the simulation
# plot the activity with given initial
plt.plot(pars['range_t'], r, 'r', alpha=0.1 + 0.1 * ie,
label=r'r$_{\mathrm{init}}$=%.4f' % (x_fps[1]))
plt.xlabel('t (ms)')
plt.title('Two steady states?')
plt.ylabel(r'$r$(t)')
plt.legend(loc=[1.01, -0.06], fontsize=14)
plt.show()
See Bonus Section 1 to cover how to determine the stability of fixed points in a quantitative way.
Think! 2: Inhibitory populations#
Throughout the tutorial, we have assumed \(w> 0 \), i.e., we considered a single population of excitatory neurons. What do you think will be the behavior of a population of inhibitory neurons, i.e., where \(w> 0\) is replaced by \(w< 0\)?
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Inhibitory_populations_Discussion")
Summary#
Estimated timing of tutorial: 1 hour, 25 minutes
In this tutorial, we have investigated the dynamics of a rate-based single population of neurons.
We learned about:
The effect of the input parameters and the time constant of the network on the dynamics of the population.
How to find the fixed point(s) of the system.
We build on these concepts in the bonus material - check it out if you have time. You will learn:
How to determine the stability of a fixed point by linearizing the system.
How to add realistic inputs to our model.
Bonus#
Bonus Section 1: Stability analysis via linearization of the dynamics#
Video 3: Stability of fixed points#
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Stability_of_fixed_points_Bonus_Videos")
Here we will dive into the math of how to figure out the stability of a fixed point.
Just like in our equation for the feedforward network, a generic linear system \(\frac{dx}{dt} = \lambda (x - b)\), has a fixed point for \(x=b\). The analytical solution of such a system can be found to be:
Now consider a small perturbation of the activity around the fixed point: \(x(0) = b + \epsilon\), where \(|\epsilon| \ll 1\). Will the perturbation \(\epsilon(t)\) grow with time or will it decay to the fixed point? The evolution of the perturbation with time can be written, using the analytical solution for \(x(t)\), as:
if \(\lambda < 0\), \(\epsilon(t)\) decays to zero, \(x(t)\) will still converge to \(b\) and the fixed point is “stable”.
if \(\lambda > 0\), \(\epsilon(t)\) grows with time, \(x(t)\) will leave the fixed point \(b\) exponentially, and the fixed point is, therefore, “unstable” .
Similar to what we did in the linear system above, in order to determine the stability of a fixed point \(r^{*}\) of the excitatory population dynamics, we perturb Equation (1) around \(r^{*}\) by \(\epsilon\), i.e. \(r = r^{*} + \epsilon\). We can plug in Equation (1) and obtain the equation determining the time evolution of the perturbation \(\epsilon(t)\):
where \(F'(\cdot)\) is the derivative of the transfer function \(F(\cdot)\). We can rewrite the above equation as:
That is, as in the linear system above, the value of
determines whether the perturbation will grow or decay to zero, i.e., \(\lambda\) defines the stability of the fixed point. This value is called the eigenvalue of the dynamical system.
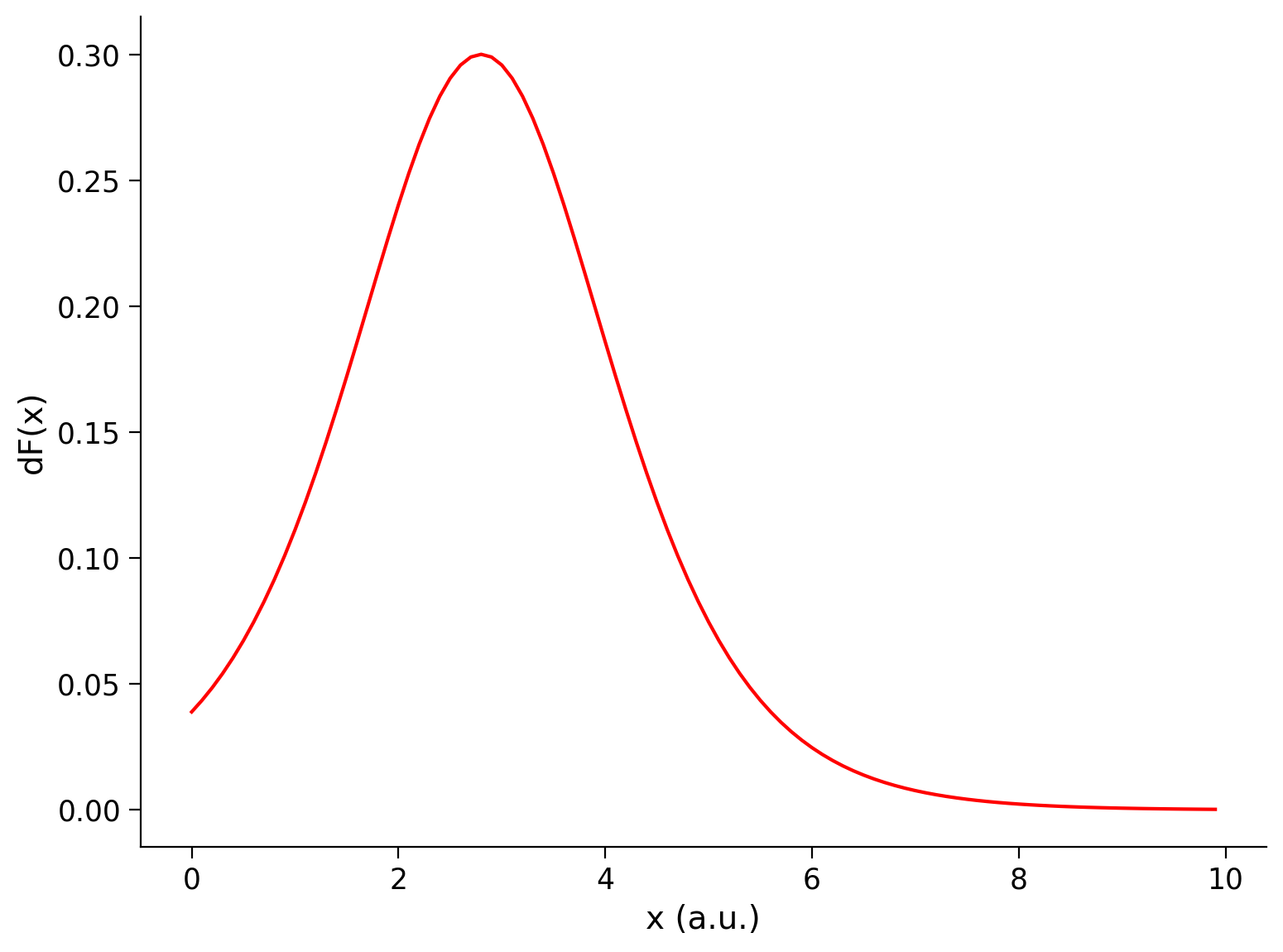
The derivative of the sigmoid transfer function is:
We provide a helper function dF which computes this derivative.
Execute this cell to enable helper function dF and visualize derivative
Show code cell source
# @markdown Execute this cell to enable helper function `dF` and visualize derivative
def dF(x, a, theta):
"""
Population activation function.
Args:
x : the population input
a : the gain of the function
theta : the threshold of the function
Returns:
dFdx : the population activation response F(x) for input x
"""
# Calculate the population activation
dFdx = a * np.exp(-a * (x - theta)) * (1 + np.exp(-a * (x - theta)))**-2
return dFdx
# Set parameters
pars = default_pars_single() # get default parameters
x = np.arange(0, 10, .1) # set the range of input
# Compute derivative of transfer function
df = dF(x, pars['a'], pars['theta'])
# Visualize
plot_dFdt(x, df)
Bonus Coding Exercise 1: Compute eigenvalues#
As discussed above, for the case with \(w=5.0\) and \(I_{\text{ext}}=0.5\), the system displays three fixed points. However, when we simulated the dynamics and varied the initial conditions \(r_{\rm init}\), we could only obtain two steady states. In this exercise, we will now check the stability of each of the three fixed points by calculating the corresponding eigenvalues with the function eig_single. Check the sign of each eigenvalue (i.e., stability of each fixed point). How many of the fixed points are stable?
Note that the expression of the eigenvalue at fixed point \(r^*\):
def eig_single(fp, tau, a, theta, w, I_ext, **other_pars):
"""
Args:
fp : fixed point r_fp
tau, a, theta, w, I_ext : Simulation parameters
Returns:
eig : eigenvalue of the linearized system
"""
#####################################################################
## TODO for students: compute eigenvalue and disable the error
raise NotImplementedError("Student exercise: compute the eigenvalue")
######################################################################
# Compute the eigenvalue
eig = ...
return eig
# Find the eigenvalues for all fixed points
pars = default_pars_single(w=5, I_ext=.5)
r_guess_vector = [0, .4, .9]
x_fp = my_fp_finder(pars, r_guess_vector)
for fp in x_fp:
eig_fp = eig_single(fp, **pars)
print(f'Fixed point1 at {fp:.3f} with Eigenvalue={eig_fp:.3f}')
SAMPLE OUTPUT
Fixed point1 at 0.042 with Eigenvalue=-0.583
Fixed point2 at 0.447 with Eigenvalue=0.498
Fixed point3 at 0.900 with Eigenvalue=-0.626
Submit your feedback#
Show code cell source
# @title Submit your feedback
content_review(f"{feedback_prefix}_Compute_eigenvalues_Bonus_Exercise")
We can see that the first and third fixed points are stable (negative eigenvalues) and the second is unstable (positive eigenvalue) - as we expected!
Bonus Section 2: Noisy input drives the transition between two stable states#
As discussed in several previous tutorials, the Ornstein-Uhlenbeck (OU) process is usually used to generate a noisy input into the neuron. The OU input \(\eta(t)\) follows:
Execute the following function my_OU(pars, sig, myseed=False) to generate an OU process.
Execute to get helper function my_OU and visualize OU process
Show code cell source
# @markdown Execute to get helper function `my_OU` and visualize OU process
def my_OU(pars, sig, myseed=False):
"""
A functions that generates Ornstein-Uhlenback process
Args:
pars : parameter dictionary
sig : noise amplitute
myseed : random seed. int or boolean
Returns:
I : Ornstein-Uhlenbeck input current
"""
# Retrieve simulation parameters
dt, range_t = pars['dt'], pars['range_t']
Lt = range_t.size
tau_ou = pars['tau_ou'] # [ms]
# set random seed
if myseed:
np.random.seed(seed=myseed)
else:
np.random.seed()
# Initialize
noise = np.random.randn(Lt)
I_ou = np.zeros(Lt)
I_ou[0] = noise[0] * sig
# generate OU
for it in range(Lt - 1):
I_ou[it + 1] = (I_ou[it]
+ dt / tau_ou * (0. - I_ou[it])
+ np.sqrt(2 * dt / tau_ou) * sig * noise[it + 1])
return I_ou
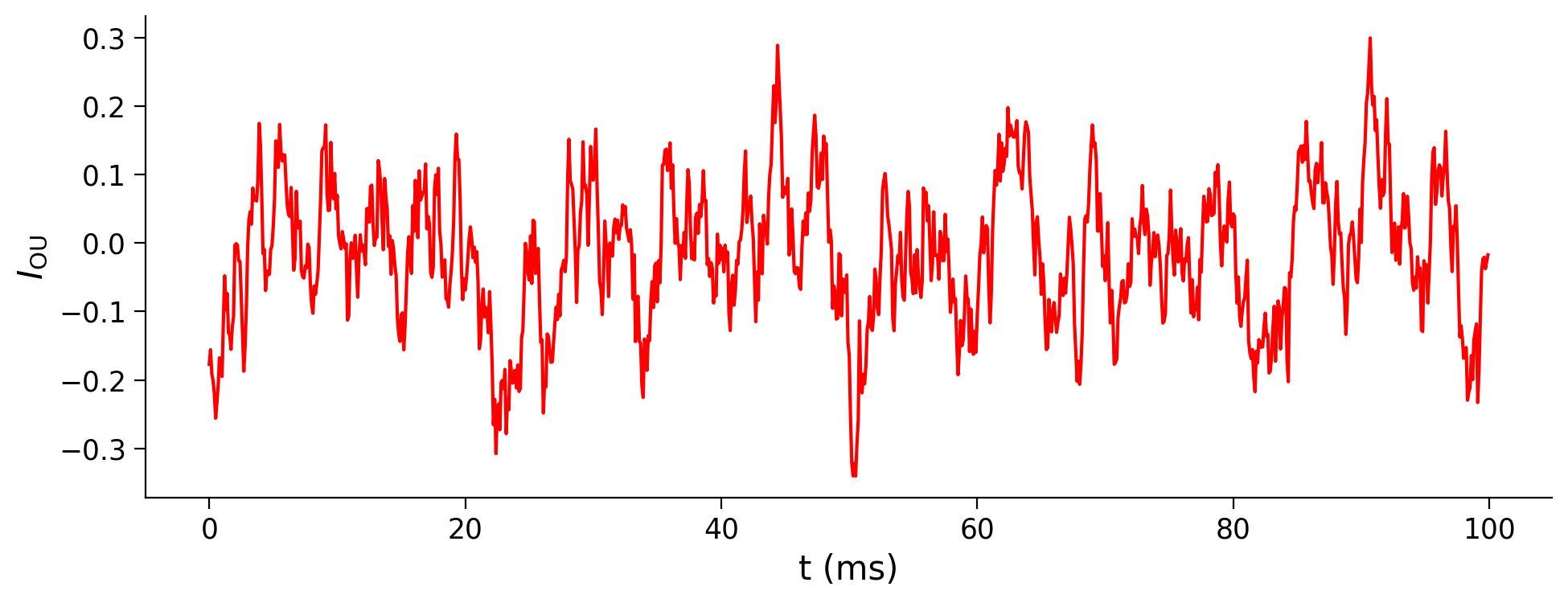
pars = default_pars_single(T=100)
pars['tau_ou'] = 1. # [ms]
sig_ou = 0.1
I_ou = my_OU(pars, sig=sig_ou, myseed=2020)
plt.figure(figsize=(10, 4))
plt.plot(pars['range_t'], I_ou, 'r')
plt.xlabel('t (ms)')
plt.ylabel(r'$I_{\mathrm{OU}}$')
plt.show()
In the presence of two or more fixed points, noisy inputs can drive a transition between the fixed points! Here, we stimulate an E population for 1,000 ms applying OU inputs.
Execute this cell to simulate E population with OU inputs
Show code cell source
# @markdown Execute this cell to simulate E population with OU inputs
pars = default_pars_single(T=1000)
pars['w'] = 5.0
sig_ou = 0.7
pars['tau_ou'] = 1. # [ms]
pars['I_ext'] = 0.56 + my_OU(pars, sig=sig_ou, myseed=2020)
r = simulate_single(pars)
plt.figure(figsize=(10, 4))
plt.plot(pars['range_t'], r, 'b', alpha=0.8)
plt.xlabel('t (ms)')
plt.ylabel(r'$r(t)$')
plt.show()
You can see that the population activity is changing between fixed points (it goes up and down)!

